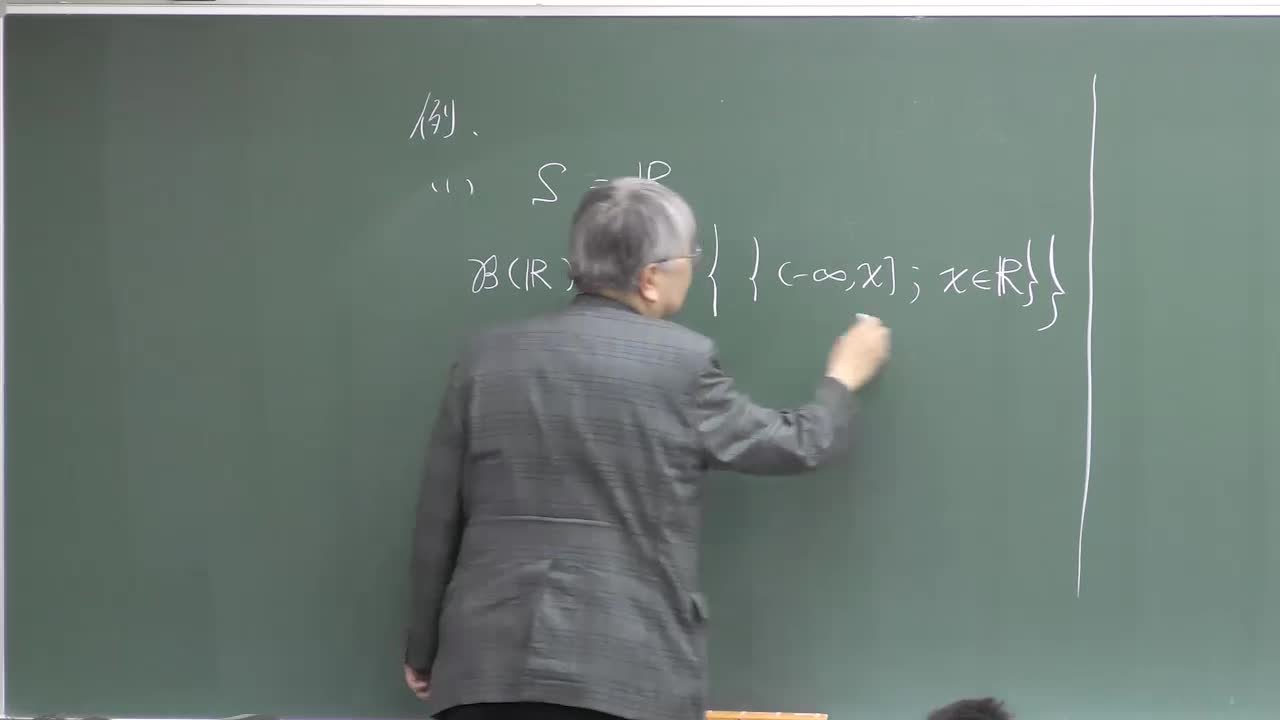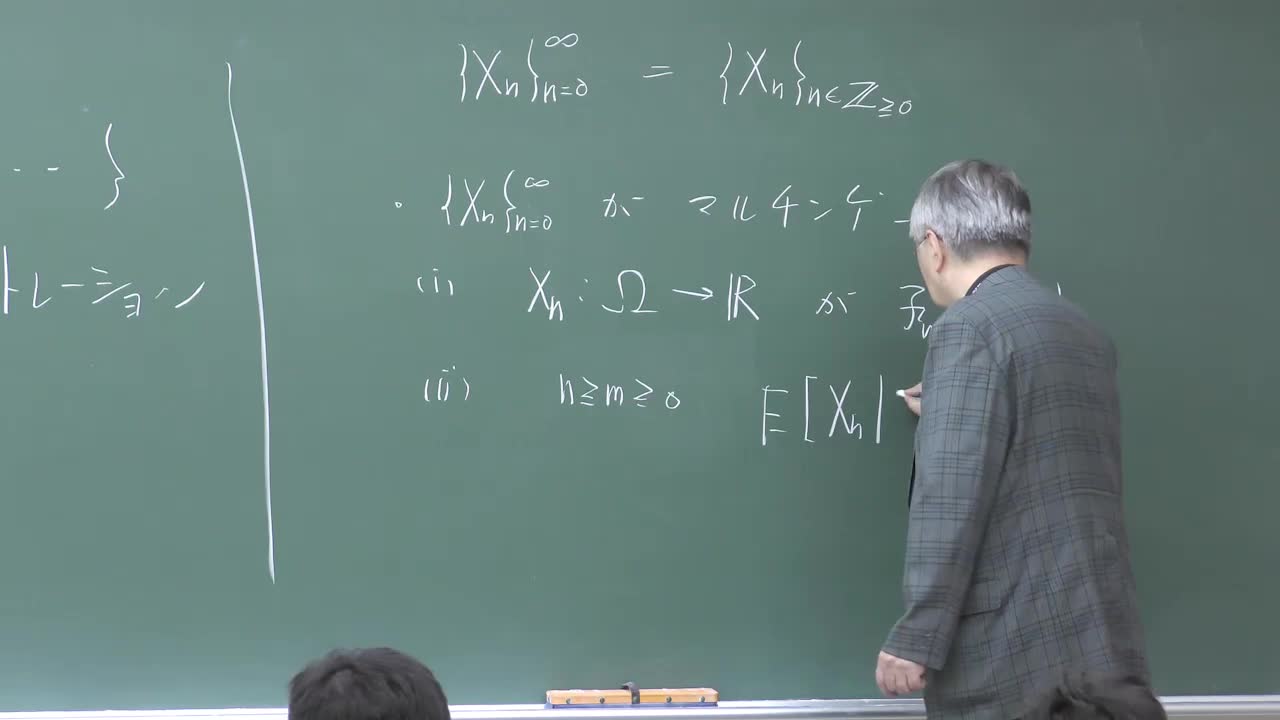HOME > 講義を探す > 講師一覧 > 講義一覧

楠岡 成雄 講義一覧

楠岡 成雄
数理科学研究科
※所属・役職は登壇当時のものです。
数理手法IV - 12　応用②
数理手法IV
第12回 数理手法IV - 12　応用②
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 11　応用①
数理手法IV
第11回 数理手法IV - 11　応用①
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 10　測度論的確率論
数理手法IV
第10回 数理手法IV - 10　測度論的確率論
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 9　測度論からの準備②
数理手法IV
第9回 数理手法IV - 9　測度論からの準備②
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 8　マルチンゲールの理論④・測度論からの準備①
数理手法IV
第8回 数理手法IV - 8　マルチンゲールの理論④・測度論からの準備①
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 7　マルチンゲールの理論③
数理手法IV
第7回 数理手法IV - 7　マルチンゲールの理論③
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 6　マルチンゲールの理論②
数理手法IV
第6回 数理手法IV - 6　マルチンゲールの理論②
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 5　マルチンゲールの理論①
数理手法IV
第5回 数理手法IV - 5　マルチンゲールの理論①
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 4　条件付期待値
数理手法IV
第4回 数理手法IV - 4　条件付期待値
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 3　確率論の基礎②
数理手法IV
第3回 数理手法IV - 3　確率論の基礎②
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 2　確率論の基礎①
数理手法IV
第2回 数理手法IV - 2　確率論の基礎①
楠岡 成雄
コースを表示 マイリストに追加
数理手法IV - 1　初めに
数理手法IV
第1回 数理手法IV - 1　初めに
楠岡 成雄
コースを表示 マイリストに追加
確率微分方程式のアイデア
数学ー革新の歴史と伝統の力（学術俯瞰講義）
第6回 確率微分方程式のアイデア
楠岡 成雄
コースを表示 マイリストに追加
確率過程モデルとしての双六
数学ー革新の歴史と伝統の力（学術俯瞰講義）
第5回 確率過程モデルとしての双六
楠岡 成雄
コースを表示 マイリストに追加
伊藤解析とファイナンス
数理の世界－新世紀の数学を探る（学術俯瞰講義）
第10回 伊藤解析とファイナンス
楠岡 成雄
コースを表示 マイリストに追加
ファイナンスの実務的な問題と高い次元の積分計算
数理の世界－新世紀の数学を探る（学術俯瞰講義）
第9回 ファイナンスの実務的な問題と高い次元の積分計算
楠岡 成雄
コースを表示 マイリストに追加
< 1 >
学部・研究科
講義映像
講義言語
学年
分野
特集
絞り込み