「見ず知らずの他人に自分のクレジットカードのセキュリティが破られた!」
「SNSで他人に秘密にしたい内容を話したのに、知らない人に内容を知られていた!」
普段生活していてこのようなトラブルに滅多に遭遇しないのは、暗号が私たちの生活を支えてくれているおかげなのです。
では、そもそも暗号とはどのようなものなのでしょうか?
UTokyo OCW広報部長のだいふくちゃんに聞いてみると、こんな暗号をくれました!
みなさんが「暗号」と聞くと思い浮かぶイメージに近いかもしれませんね。

せっかくなので、この暗号を一緒に解いてみましょう!
昔ながらの暗号
あまり手がかりがなくて難しいですが…何もできないでいるよりは、とりあえずこの暗号は「伝えたい文章をローマ字に直して、アルファベット順に同じ数だけずらしたもの」だと考えて進めてみましょう。
たとえば、「IB」や「XP」や「HB」といった部分は短いので何かわかるかもしれないですね。
日本語のローマ字なら、単語の最後が「A I U E O」で終わるのが自然な気がするので、「B」や「P」を「A I U E O」などにずらしたときに文章の意味が通じるか考えてみましょう。
「A I U E O」のなかで「B」にいちばん近いアルファベットは「A」ですね。
「B」は「A」のひとつ後のアルファベットですが、「P」のひとつ前のアルファベットは「O」なので、これも「A I U E O」に含まれていますね。どうやらこの暗号は、伝えたいメッセージのローマ字をひとつ後のアルファベットに置き換えたもののようです。
では、暗号のアルファベットをひとつずつ前にずらしてみましょう。

「だいふくちゃん通信は 楽しく 東大の授業を知ることができる 心躍るメディアです」となり、意味が通じました!どうやら暗号の解読に成功したみたいです。
だいふくちゃんは「暗号」といえばこのような暗号を思い浮かべるようですが、では現代社会でこのような暗号を使って安全に暮らすことができるのでしょうか?
現代社会で使われている暗号
だいふくちゃんが考えてくれた暗号は「伝えたい内容をローマ字にして、アルファベット順に従って決まった文字数だけずらしてできた文章」でしたね。
もし、ネットショッピングなどでクレジットカード情報をこの暗号方式で伝えると、数字なら10通り、アルファベットなら26通り試せば突破されてしまいます。パソコンで計算すれば一瞬です。悪意をもった盗聴者にすぐにバレてしまうので、安全とはいえませんね。
だいふくちゃんの暗号のよくなかったところを考えてみましょう。まず挙げられるのは、内容を伝えたい相手にも暗号化の方法が秘密なので、伝えたい相手が正しく暗号を解くという確証がないことです。
これは逆にいえば、内容を知られたくない相手にも内容を知られてしまう可能性がある、ということです。現代社会は秘密にしたいことだらけなので、これは良くないですね。
では、暗号化の方法は公開しつつ、特定の相手にだけ秘密の情報を渡すにはどうすれば良いのでしょうか?
現代社会では、公開鍵暗号という方式の暗号が使われています。公開鍵暗号とは、暗号化に使う鍵を公開し、それを解読(専門的には複号という)するための鍵は秘密にする、という方式です。役割の違う鍵が2つあるのがポイントです!
鍵を公開してしまっても安全なの?と思った方もいらっしゃるかもしれませんが、これがなんと大丈夫なのです。どのような仕組みでそれを実現するのかはさておき、図解してみます。
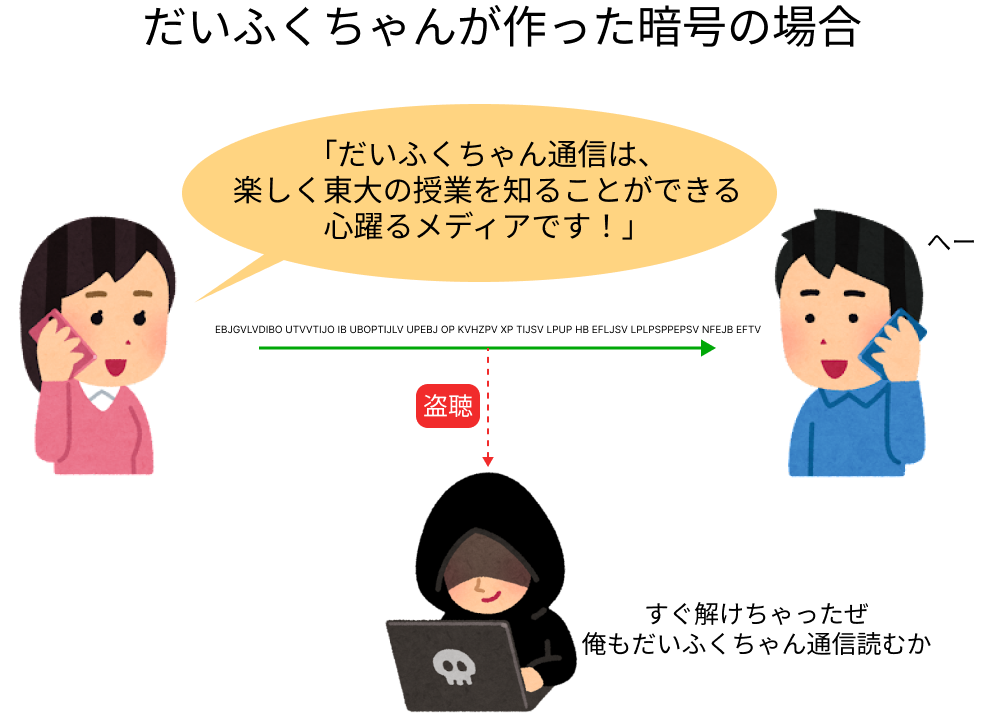
先ほども説明したとおり、だいふくちゃんが作った暗号の場合は暗号化の方法さえわかってしまえばパソコンですぐ解けてしまいます。では現代社会で使われている暗号である公開鍵暗号ではどうなるのでしょう?
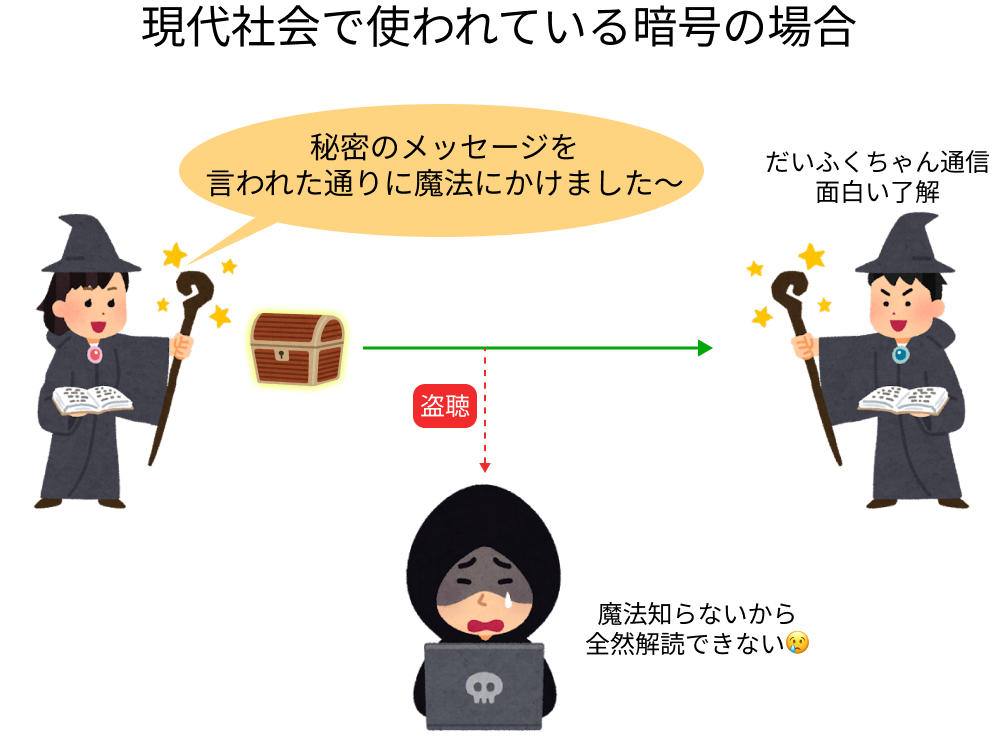
公開鍵暗号は、「メッセージを暗号にする魔法の合言葉」と「暗号をメッセージに戻す魔法の合言葉」が別々なので、「メッセージを暗号にする魔法の合言葉」だけ公開しておけば、もう一つの魔法を知られなければ安全、というわけです。通信を盗聴されたとしても、盗聴者は暗号をメッセージに戻す魔法を知らないので、解読できないわけですね。
では、このような2つの対になる「魔法」をどのようにして作れば良いのでしょうか?
RSA暗号
暗号が安全であるためには、暗号文をメッセージに戻す操作が盗聴者にとってとても時間がかかる作業でなくてはなりません。しかし、受信者にとってはその操作は簡単じゃないと困ります。でも送信主は、メッセージをわざわざ面倒臭い手順で暗号文にしたくはありませんよね。
これらのバランスがちょうどよい「魔法」が、数学の世界には存在します。素因数分解です。難しい言葉が出てきたので、簡単に説明しますね。
まず、11×34を計算してみてください。筆算を使えば電卓がなくてもすぐに答えが374だとわかると思います。
では次に、先ほど「11 × 34 = 374」と求めましたが、そのような感じで、「?×? = 57」となるような、「?」に当てはまる2つの整数を求めてみてください(2つの?にはそれぞれ異なる数字が入ります)。簡単すぎる方は57の代わりに893で計算してみてもいいかもしれません。
最初に出題した掛け算と違って、後に出題した「?」を求める問題は難しかったと思います。普通の電卓でも計算できないでしょう。
このように、あるひとつの数が与えられて、その数に対応した「?」を求めることを素因数分解と言います。今までに説明してきた状況では、与えられる数をうまく作れば素因数分解の答えは1つしかないことが知られています。
この素因数分解の逆の計算である整数の掛け算は、すぐに計算できましたよね。でも素因数分解は難しかった。数字の桁が大きくなれば、より一層掛け算と素因数分解の面倒臭さはかけ離れていきます。このような、計算の難しさが行きと帰りで大きく異なる一方向性のある計算は、安全な公開鍵暗号に求められる資質を満たしています。
実際に素因数分解の難しさを根拠として暗号が開発され、この理論に基づく暗号はRSA暗号と呼ばれています。(その具体的な仕組みまで説明すると長くなりすぎてしまうので、他の記事を参照していただければと思います。)RSA暗号は現代社会の多くの側面での暗号通信を支えており、今や私たちの生活になくてはならない技術となっています。
しかし実は、長年私たちの安全な暗号通信を支えてきたRSA暗号にも重大な欠点があるのです…!
RSA暗号を脅かす技術
RSA暗号の欠点を2つ紹介します。
1つめは、素因数分解が困難ということの数学的な証明がまだ発見されていないという問題です。どういうことかというと、素因数分解を効率よく計算する方法を世界のどこかでものすごく賢い誰かが発見してしまうかもしれないということです。
2つめは、量子コンピュータという次世代のコンピュータを使うと、RSA暗号を従来の方法よりも素早く解くことができるようになる、という問題です。この方法は非常に難解なので、今回は説明しませんが、興味のある方は「Shorのアルゴリズム」と検索してみてください!
近年、量子コンピュータの実用化に向けて世界中の研究者がハードウェア開発に取り組んでいます。世界中の暗号の標準になっているRSA暗号が安全と言えなくなるのは時間の問題、なのかもしれません。
量子鍵配送 – 未来社会を支える暗号技術
では私たちのプライバシーはもう守れないかというと、実はそうでもないようです。今回紹介するのは、量子鍵配送という技術です。
さっきから量子という言葉が時々出てくるので気になっていた方も多いかもしれませんが、量子とはもともと物理学で研究されてきたものです。量子暗号を理解する上で非常に重要な概念なので、しっかり解説します。
量子とはなんなのか
古典的な物理学の長年の研究の結果、世界の全ての運動は粒の理論と波の理論の2つで説明できる、という結論に辿り着きつつありました。ここでいう粒に該当するものには、例えば野球ボールなどがあります。野球ボールを投げるタイミング、投げる角度、投げるスピードを知ることができれば、いつ、どこに着地するのか予測できそうです。粒の理論はこの予測を可能にしました。
一方で波の理論で予測できるものは、例えば水面に石を投げ入れた時に波紋がどんな広がり方をするかといった問題です。石が水面に落ちる瞬間と、その時の水面の揺れ具合が分かれば、10秒後に波紋がどんな大きさでどれくらい激しく揺れているのか予測することができます。
確かに野球ボールと水面の動きは全然違うし、野球ボールの運動を波だと捉えてうまくいく訳がないことも、水面の運動を粒と捉えることが難しいこともわかると思います。古典的な物理学では、波と粒は全く別々の概念でしたし、複雑な現象も分解していけば必ずこの2要素で説明できると考えられていました。
しかしそんな中、波とも粒とも言えない微妙な存在があることがわかりました。光です。光は波に独特の性質である干渉という現象を起こすため、素直に考えれば波のように思えます。しかし一方で、光の強度を弱めていくと光は連続的には弱くならず、飛び飛びの強度になることがわかりました。この事情を考えると、光はエネルギー単位の塊の粒として扱うほうが飛び飛びの性質を扱うのに都合が良さそうです。では光とは一体なんなのでしょうか?
現代物理学では、光が粒か波かといった論争はしない代わりに、量子という新しい概念を導入します。量子は波と粒の2つの性質を同時に持つことのできる概念です。
量子1つがどんな動きをするのか見てみましょう。
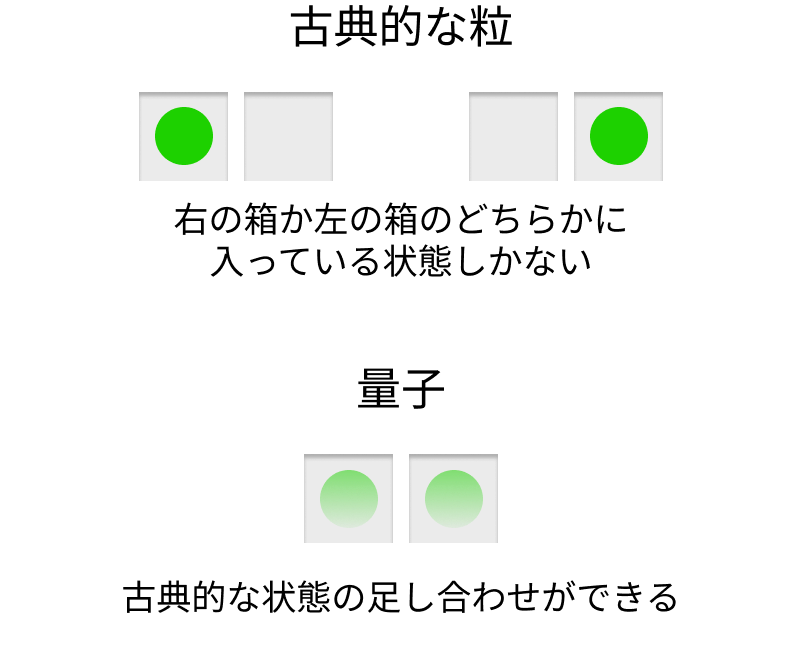
粒が2つの箱のどちらかに入っているという状況を考えます。古典的な粒、例えば野球ボールといった私たちの直感に沿う物体は、右か左の箱のどちらかに入っている状態を取ることができ、それ以外の状態はありえません。
一方、量子はそのような状態を重み付きで足し合わせることができます。でも誰もこのような状態を見たことはないですよね。それはどうしてなのでしょう?
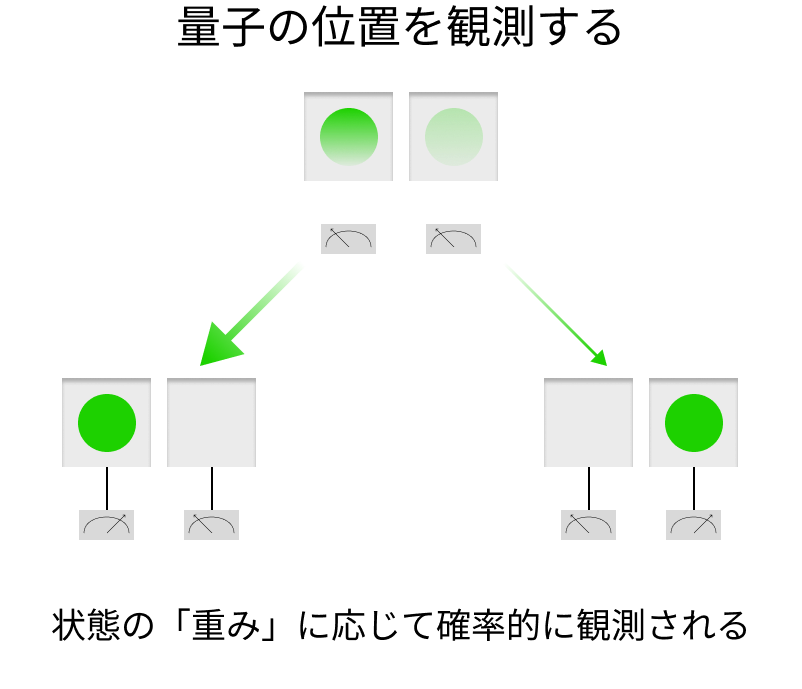
実は、量子の場所を測定しようとすると、その重みに応じた確率で位置が決まってしまうという性質があるのです。つまり観測によって「2つの状態が足し合わされた状態」が壊され、足し合わされる前の状態のどちらかに確率的に変化してしまうのです。
もっとたくさんの状態を重ね合わせることもできます。箱の場所がとても小さくなると、あたかも波のように見えますね。
実はこのような「状態の重みの波」の動きは以前の物理学で知られていた挙動によく似ていることもわかりました。これが粒と波の二重性のざっくりとしたイメージです。もちろん、このような重ね合わせ状態でも位置を決定しようとすると状態が壊れます。
量子鍵配送のイメージ
量子鍵配送ではこのような量子の性質をたくみに利用しています。先ほどの公開鍵暗号とは異なり、メッセージを解読する鍵とメッセージを暗号文にする鍵が同じであるような暗号を使うとします。送信者が受信者に鍵を送ろうとしている、という状況を考えてみましょう。量子に鍵の情報を載せて送っている場合、盗聴者は盗聴のために量子を観測する必要があります。
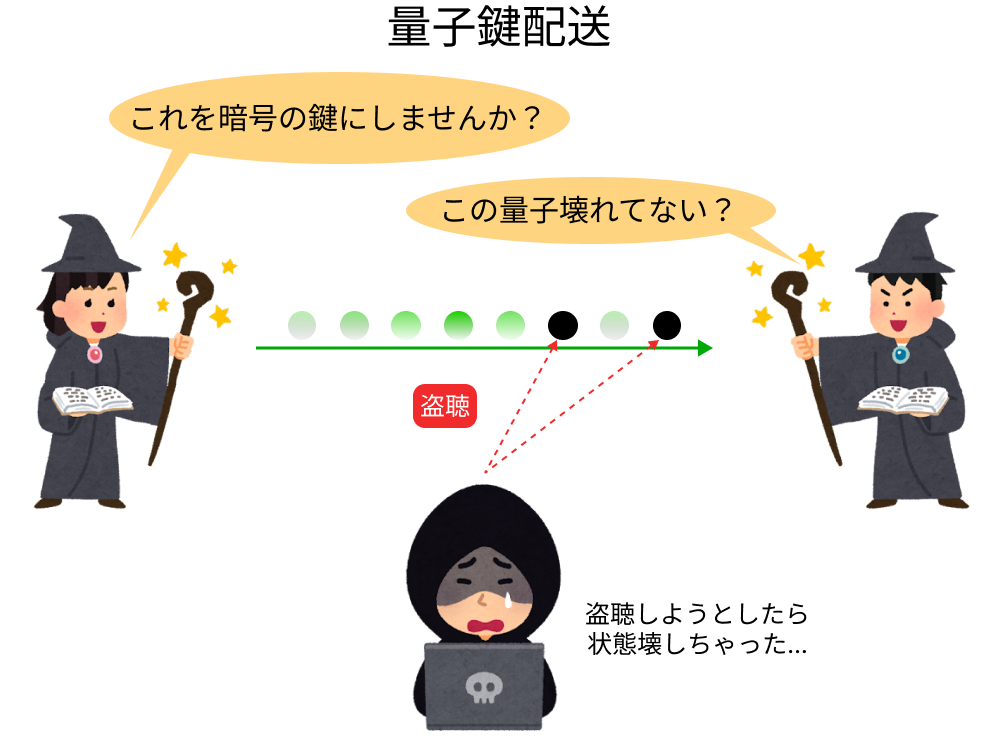
盗聴者によって量子が壊されたかは見分けることができ、盗聴されたかどうかがわかってしまいます。量子コンピュータでも解読が困難な暗号と盗聴されなかった鍵を使えば、RSA暗号よりもっと安全な暗号通信ができるというわけです。
このようにして鍵の候補の情報を量子に乗せて安全な通信を作る技術を量子鍵配送といいます。ついに、物理法則という、誰もが破ることのできない規則のレベルで安全な暗号通信が考案されたのです!
終わりに
今回は、暗号という技術の歴史を俯瞰し、実用化が待たれる最先端の暗号について紹介しました。物理学と数学が協力し合い、新しい暗号を形作りつつあるということを皆さんに知っていただければ幸いです。
「量子鍵配送の際に盗聴されたかどうか見分けるにはどういう通信方法にすれば良いの?」
「量子暗号はいつ実用化されるの?」
「実際の通信装置はどんな感じ?」
「やっぱり量子ってのがよくわからない!」
この記事をここまで読んでくださった皆さんは、きっと上のような疑問を持たれていることでしょう。
この記事では触れられなかった多くの数学的・物理的事情も全部ひっくるめて「量子論や暗号について勉強してみたい!」という方には、UTokyo OCWで誰でも閲覧できる、2012年の小芦先生の授業動画「微弱光を用いた究極の暗号」がおすすめです。こちらの授業動画では、光を使った量子暗号の作り方について説明されています。難しい数学の証明などはほとんどなく、量子の振る舞いや暗号としての利用方法を楽しく学ぶことができます!
UTokyo OCWではこのほかにも、最先端の研究を行っている研究者による、わかりやすく内容も充実した講義動画をたくさん提供しています。これらの講義動画は誰でも無料で、会員登録なしで閲覧可能です。皆さんのご利用をお待ちしております!
今回紹介した講義:光の科学−未来を照らす究極の技術とアイデア(学術俯瞰講義)第11回 微弱光を用いた究極の暗号 小芦 雅斗先生







