みなさんは「3囚人問題」というものをご存知ですか？

それは、次のような問題です。

……

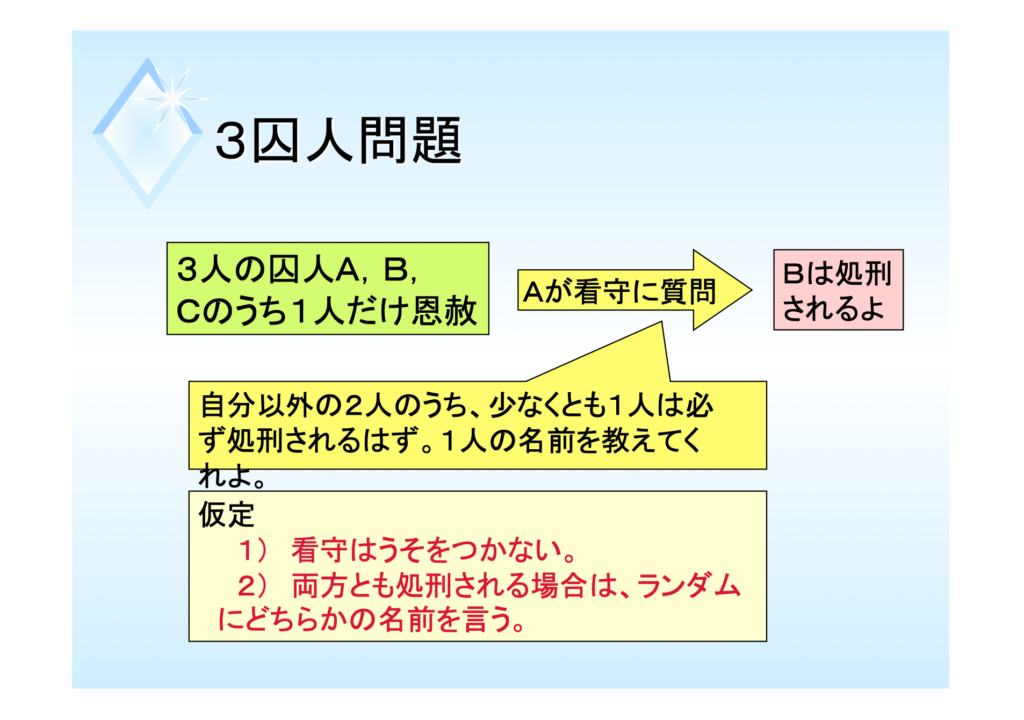
いま、3人の囚人A、B、Cが監獄に閉じ込められ、処刑を待っています。

恐怖に震えながら処刑を待つ3人のもとに、看守が現れてこう言いました。

「君たち3人のうち1人を恩赦にする」

つまり、A、B、Cの囚人それぞれが、3分の1の確率で、処刑を免れることができるのです。3人の囚人は喜びましたが、まだ処刑される確率は3分の2もあります。

囚人Aは、看守に「B、Cのうち、処刑される人を教えてくれ」と聞きました。

すると看守は、「Bは処刑される」と答えました。

ということはつまり、AかCのうち、どちらかは恩赦になるということです。

囚人Aは、自分が助かる確率が3分の1から2分の1になったと喜びました。

しかし、本当にそうでしょうか？囚人Aが恩赦になる確率は、本当に2分の1に上がったのでしょうか？

以上が、3囚人問題です。同型の「モンティ・ホール問題」の方を知っている人もいるかもしれません。（知らない方は検索してみてください）

実はこの問題、確率は3分の1のまま変わらないのです。

しばしば、確率というのは私たちの直感に反することがあります。

どうして確率が3分の1のままなのでしょうか。この確率は（全パターン）分の（A恩赦パターン）を示した以下の数式で求められるのですが……

いかがでしょうか？これを見ても、数式を理解するのが得意ではない人は、うまくイメージが掴めないかもしれません。

コロナ禍で話題になった「感染者問題」（精度が高い検査薬でも、陽性反応が出た人のうち、実際は非感染である人が相当な割合で生じうるという問題。この記事内で紹介するので、知らない方は読み進めてみてください）など、実際の確率が直感に反する例は、私たちの身近なところにあります。

数字が苦手という方でも、間違った情報に惑わされないために、なぜ実際の確率が直感に反するのか、理解しておく必要があると言えるでしょう。

今回は、3囚人問題や感染者問題などの原理について、数式を使わずに理解する方法について考える講義を紹介します。

まずは3囚人問題を数式で考える

今回講義を担当してくださるのは、教育学研究科（当時）の市川伸一先生です。

市川先生は、「視覚化」によって3囚人問題や感染者問題を解決する方法について解説します。

さて、先ほど紹介した3囚人問題ですが、数式として解く際は、「ベイズの定理」というものを使用します。（以下、数式の説明に入ります）

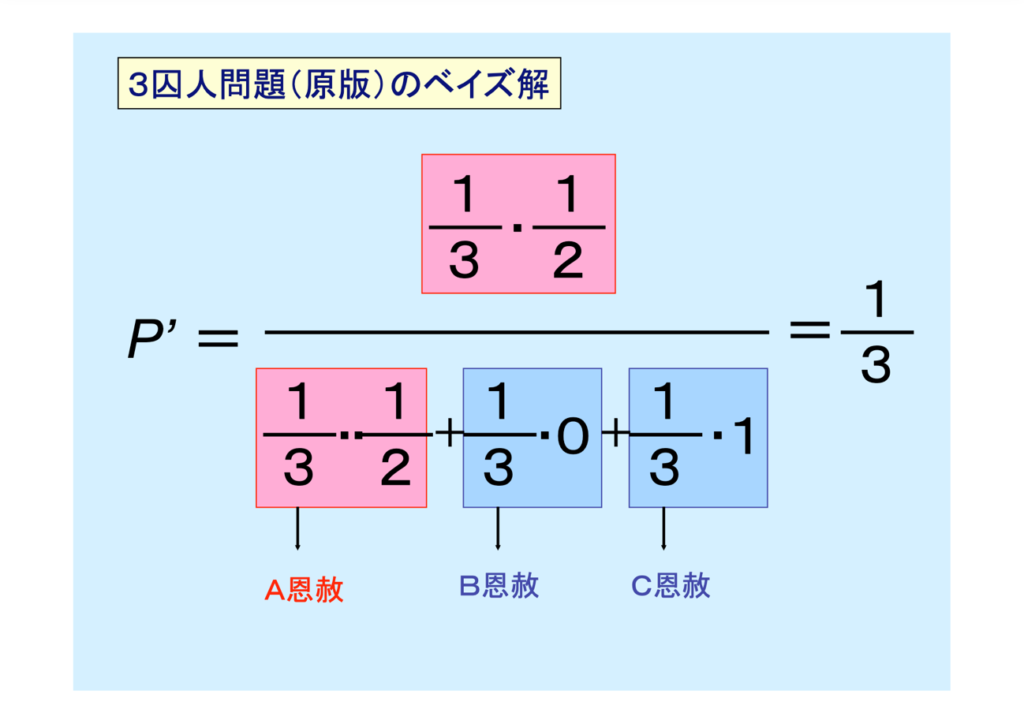
求める確率は、「Bは処刑される」と言われたときに、Aが恩赦である確率なので、

分母が

Aが恩赦であって「Bは処刑される」と言われる確率（1/3×1/2）＋Bが恩赦であって「Bは処刑される」と言われる確率（1/3×0）＋Cが恩赦であって「Bは処刑される」と言われる確率（1/3×1）

分子が

Aが恩赦であって「Bは処刑される」と言われる確率（1/3×1/2）

です。

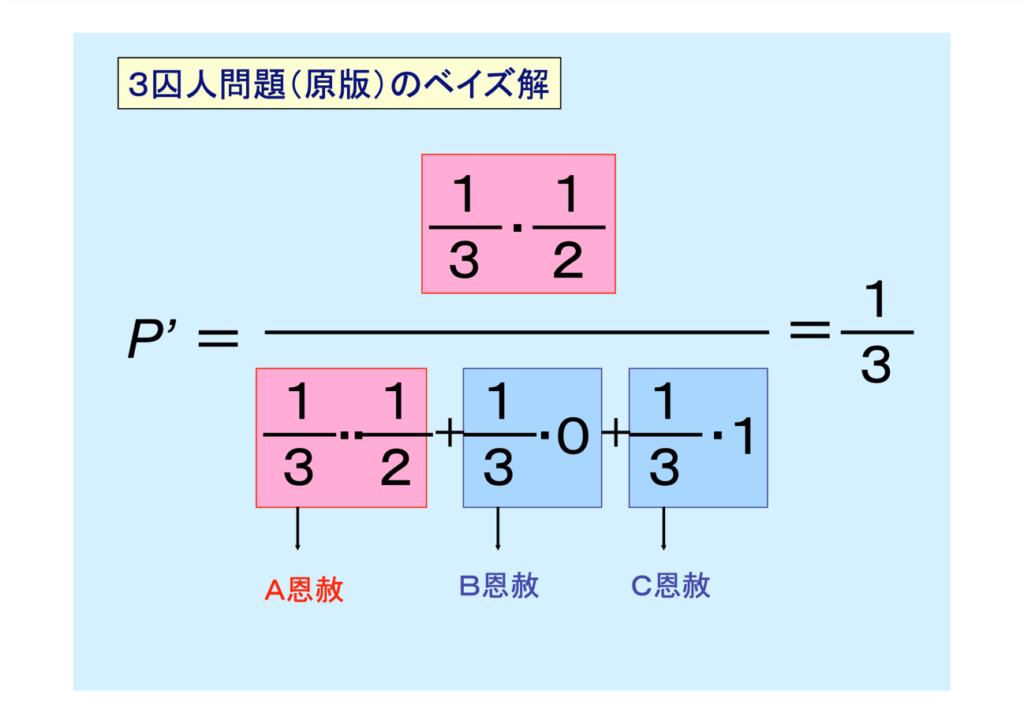
改めて数式を提示します。どうでしょう、理解できたでしょうか？

「大丈夫、ばっちりだ」という方もいる一方、「何がなんだか分からない」という方もいると思います。

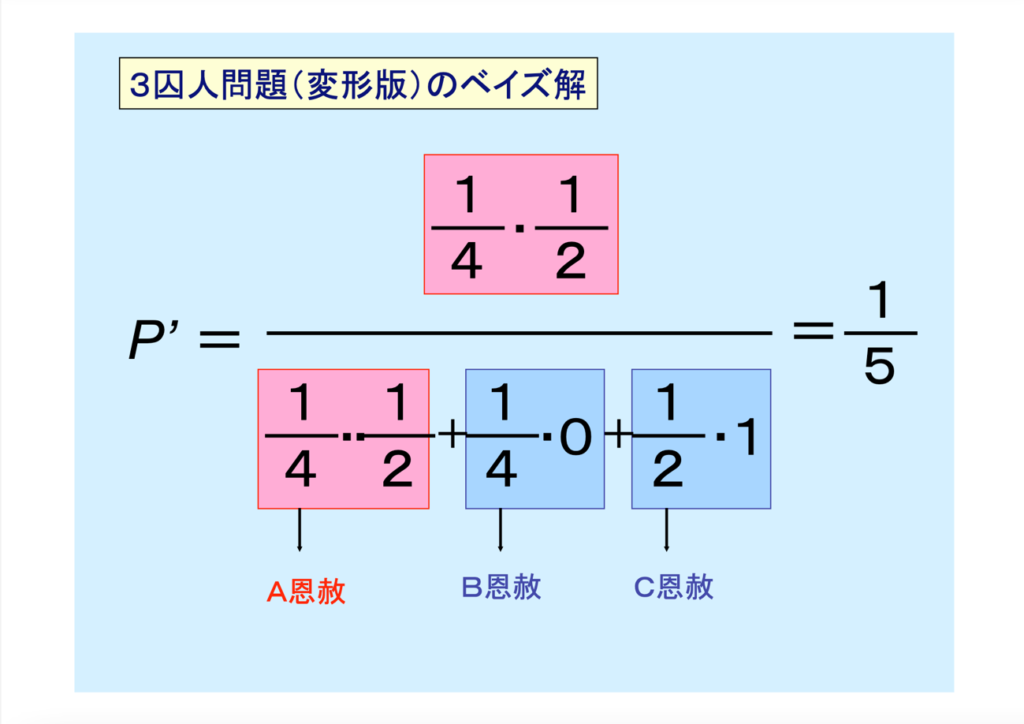
それでは、恩赦になる確率が囚人ごとに異なる場合、AとBが恩赦になる確率が4分の1で、Cが恩赦になる確率が2分の1の場合はどうでしょうか？こうなってくるとだんだん複雑になってきます。

改めて数式を提示します。どうでしょう、理解できたでしょうか？

「大丈夫、ばっちりだ」という方もいる一方、「何がなんだか分からない」という方もいると思います。

それでは、恩赦になる確率が囚人ごとに異なる場合、AとBが恩赦になる確率が4分の1で、Cが恩赦になる確率が2分の1の場合はどうでしょうか？こうなってくるとだんだん複雑になってきます。

「うー！難しいよ！」という方！安心してください。

この3囚人問題は、より分かりやすく、図で表すことができるんです。

高性能の検査薬でも偽陽性を大量に出すのはなぜ？

3囚人問題の図について説明する前に一度、別の例としてあげた感染者問題について考えてみましょう。

……

1000人に1人の割合で感染する病気があります。

その病気の検査薬は精度が高く、

検査対象となる人が感染していた場合「98%が陽性、2%が陰性」、

非感染だった場合「99%が陰性、1%が陽性」を示します。

その検査薬で陽性が出た場合、多くの人は直感的に、高い確率で感染しているのだろうと考えるはずです。

しかし、ベイズの定理で計算すると、陽性反応が出た場合の感染確率は、たった0.089（＝8.9%）しかありません。

この式の構成も、先ほど紹介した3囚人問題のベイズ解の構成と全く同じです。

「ルーレット表現」によって直感に反する確率を理解する

市川先生によれば、このような確率の問題は、「ルーレット表現」というものを用いて図解することができます。

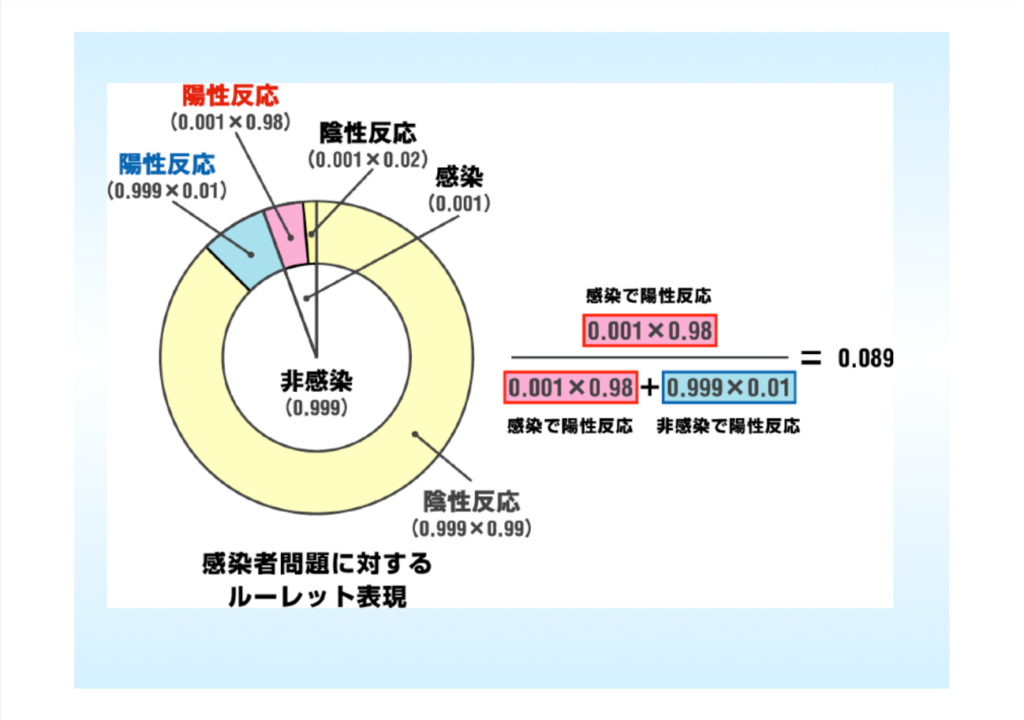
感染者問題のルーレット表現は、以下の図の通りです。

この図を見ると、非感染の陽性反応が感染の陽性反応よりも多くなっているのが分かると思います。これは、非感染の割合が圧倒的に高いためです。

このように、図解してみることで、言葉にしたときには意識しなかった要素（この場合は、非感染と感染の割合の差）がはっきりとあらわれ、確率を正しく認識することができるようになります。

このルーレット表現は、先ほどの3囚人問題でも利用することができます。みなさん、ぜひ自分で作ってみてください。

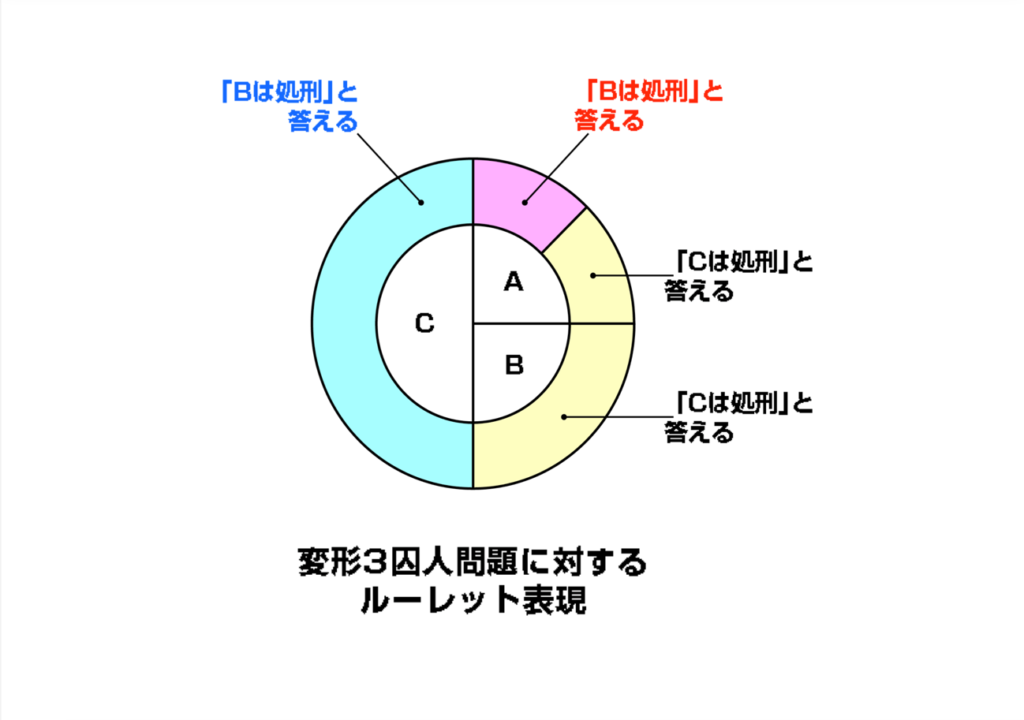
また、このルーレット表現を使えば、ただの3囚人問題だけでなく、囚人が恩赦になる確率がそれぞれ異なる変形3囚人問題を図解することもできます。

この図を見ると、「Bは処刑と答える」場合のうち、Aが恩赦になる確率が5分の1であるというのがよく分かると思います。

なぜ間違った直感を抱いてしまうのか考えるために

講義ではそのほか、割り算やツルカメ算を図解して考える方法や、条件付き確率について考える「カセットテープ問題」についても取り扱っています。

市川先生によれば、私たちは、数式と同等の情報を持つ同型図式によって、瞬時に数式が示す内容を理解する能力を持っています。

このような、人間を間違った直感に導く確率問題の研究の射程は、単なる数学の領域にとどまりません。

数学的な考え方を理解するうえでどういう手立てを取ればいいのかという点で、心理学や教育学と結びついているのです。

数学が好きだという方はもちろんですが、なかなか数式が理解できないという方にこそ、ぜひこの講義動画を視聴して、自分の考え方の「癖」を認識していただければと思います。

今回紹介した講義：心に挑む－心理学との出会い、心理学の魅力（学術俯瞰講義）第9回 学習と教育の心理学 市川 伸一先生

＜文／竹村直也（東京大学オンライン教育支援サポーター）＞