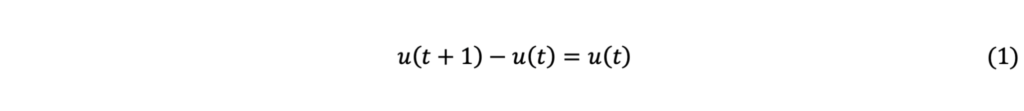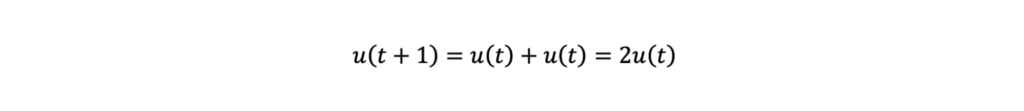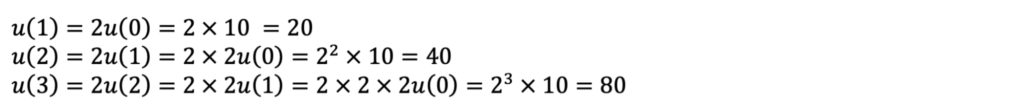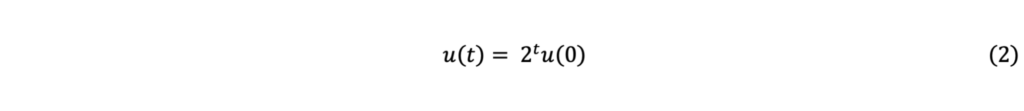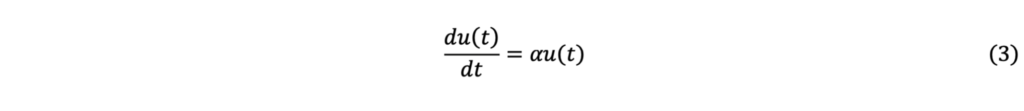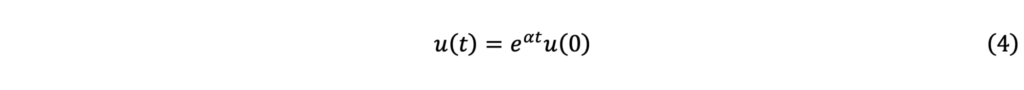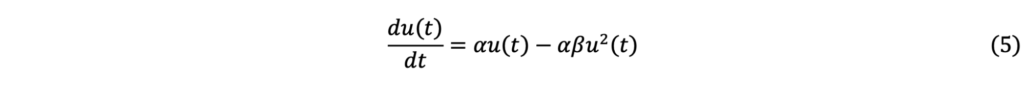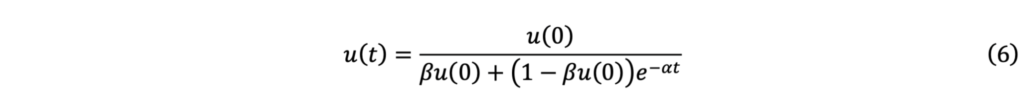高校で習う数学の分野に,微分・積分があります.
「なんか聞いたことあるけど習っていない」
「高校生のころ苦しめられた思い出が…」
「大学受験レベルなら余裕だな」
様々な方がいらっしゃると思います.
そもそも,なぜ微分・積分を勉強するのでしょうか.
もっと言うと,この学問はどのような面白さがあり,またどのように活かされていくのでしょうか.
これらは,理系の大学に進学しない限り,なかなか実感しにくいと思います.
微分・積分は,もちろん純粋に数学としての面白さもありますが,実は世の中のあらゆる現象を解析し,理解する上で欠かせないツールになっています.
今回は,薩摩先生の2つの講義から,現象の理解にどのように数学が用いられてきたかを,いくつかの現実的な例とともに覗いてみましょう.
マルサスの法則 —駒場キャンパスのねずみ—
それでは,ここで東京大学駒場キャンパスのねずみの数について,考えてみます.
自分は駒場キャンパスではねずみを見たことがないですが,ここでは仮に,今キャンパス内に10匹のねずみがいるとします.
そして,このねずみが,「1週間経つと今いる数と同じ数だけ増える」とします.
つまり,最初10匹いたのが,1週間後には10 + 10 = 20 匹になり,さらにその1週間後には20 + 20 = 40匹にまで増えます.
恐ろしいペースですね.もちろん仮の話です.
さて,もしこのペースで増殖がずっと続いた場合,ねずみの数はどうなるでしょうか?
私達は,あるタイミングにおけるねずみの数を,完璧に予測することができます.
少しだけ数式を出すことにしましょう.なるべく簡単にしますが,分からなくなったら数式の箇所のみ飛ばしていただいても構いません.
数学における慣例に倣い,ある週(ここではその数字をtと書きます)におけるねずみの数をu(t)と書くことにします.
例えば,u(2)と書いたら,これは2週間後のねずみの数を表します.
今(=0週間後)はねずみが10匹いるので,u(0) = 10 です.
ねずみは,「1週間経つと今いる数と同じ数だけ増える」ので,
となります.1週間経った時のねずみの増加数(左辺)は今いるねずみの数(右辺)に等しい,という式です.同じ意味ですが,別の書き方をすると,
ですね.1週間後には今の2倍にまで数が増えます,という式です.
試しに,1週間後から3週間後までのねずみの数を計算してみましょう.
ここで法則性を見つけると,この後はもう計算しなくて良いことに気づきます.
u(t)を知りたかったら,
を計算すれば良いわけです(これは,漸化式を習ったことがある人はすぐに分かったかもしれませんね).
例えば,20週間後の数を知りたかったら,2の20乗に10をかけて,直ちに10,485,760匹と求まります.
さて,ここまで特殊なねずみについて考えてきましたが,同じような関係性を,マルサスという経済学者が人口の増加について提唱したため,この関係性は「マルサスモデル」「マルサスの法則」とも言われます.
マルサスの法則の数学的な本質は「増加率1が今ある量に比例する」ということです.
実はそのような関係性は様々なところに見られます.複利の計算もそうですよね.
そして,この関係は,(1週間ごとの飛び飛びの値に注目するのではなく)連続的な変化に対して適用させると,次のような式で書けます.
微分が出てきました.
スペースがないため詳しく説明できませんが,意味合いは(1)式と同じようなもので,u(t)の増減率(左辺)がu(t)に比例する(右辺)という意味です.
αは単なる定数で,あまり気にしなくても良いです.
(一般に,このαは増殖率と呼ばれ,α を 1/週 とすると(1)式に対応します.)
そして,ここから一気に説明を省略しますが,(3)式を解くと以下の式になります.
(高校理系レベルの数学を未履修の方にとっては難しい式ですが,この話で大切なのは式の中身ではありませんのでご安心を.)
これは,先ほどの(2)式と同じように,あるタイミングでのuの値を予測できる式です.
(微分・積分まで学習した読者は,(3)式を直接解いて(4)式を導けるでしょう.また,より発展的な学習をされている方は,ある条件のもとで先程の漸化式の一般解の極限を取っても,この式にたどり着けるはずです.詳細は薩摩先生の講義で紹介されています.)
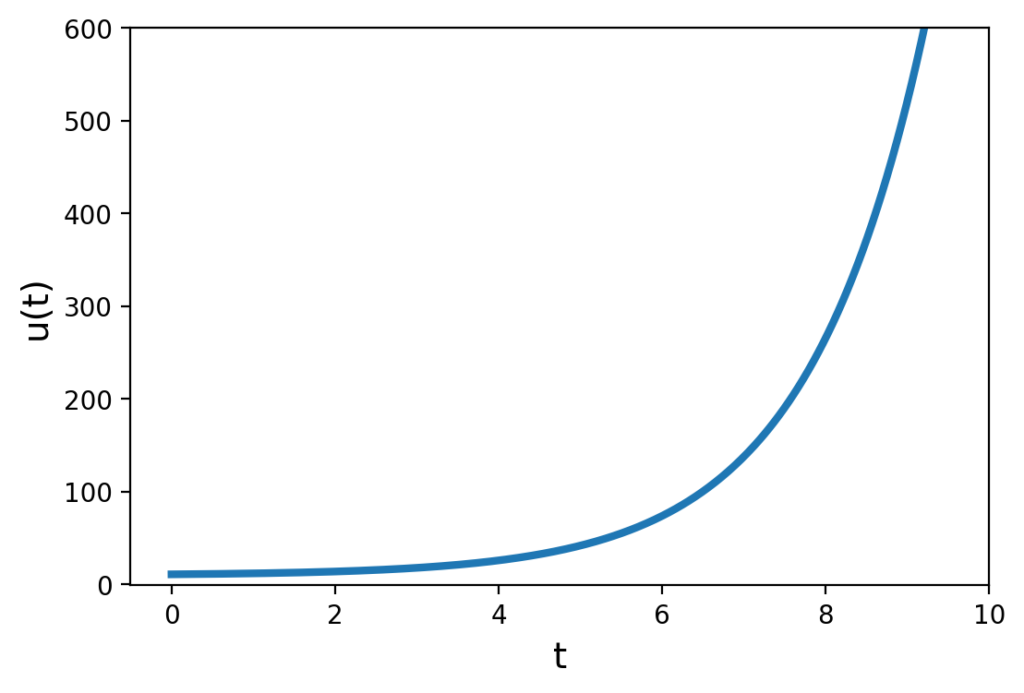
これを,グラフで可視化してみると,下の図のようになります.
爆発的にねずみが増殖していることが分かりますね.
この話で大切なことは,もし微分・積分を学習していると,「ある瞬間瞬間での数の増減のルール」が分かれば,任意のタイミングでの数を予測できる,ということです.
(3)のような式を専門的には微分方程式と言います.
人類は,何かの法則に基づいて(3)式のような微分方程式を立て,それを解いて得た(4)式のような解を見ながら,現象を理解してきたのです.
微分・積分は,300年に渡って人類が得てきた,あるいは開発してきた,強力なツールなのです.
このような考え方は,主に科学の分野において,頻繁に用いられています.
空中に放り投げられたボールはその後どこに落下するか,コイルとコンデンサで構成された電気回路に電流はどう流れるか,これらは全て微分方程式を解くことによって求められます.
講義では他にも,左右に置かれた餌に魅了されて右往左往する100匹の羊を例に取りながら,拡散方程式という名の付いた微分方程式について説明されています.
そんな羊の群れを想像して和むだけでももちろん十分ですが,数学的な興味を持たれた方はぜひ講義の方もご覧ください.
ロジスティック方程式 —爆発的には増えないねずみ—
さて,駒場キャンパスのねずみの話を聞かれた多くの方は,「そんな永遠に増え続けるねずみなんているわけないだろう」とお思いでしょう.
自分もそう思います.先程の図のようにねずみに増殖されてしまったら,駒場キャンパスは授業どころではなくなります.
もちろん,現実にはそのようなことはなかなか起こらないはずです.これはすなわち,ねずみに対する先程の仮定「1週間経つと今いる数と同じ数だけ増える」が,いついかなる時も適用されるわけではないということを意味するでしょう.
では,どうすれば良いでしょうか?
ここでは,微分方程式の考え方に立ち戻って,「ある瞬間瞬間での数の増減のルール」を,より現実的に仮定してみましょう.
先程の仮定には増加の効果しか入っていませんでしたが,数が増えすぎると天敵による捕食や餌の不足によって死んでしまう数も増えそうです.
したがって,減らす効果も微分方程式に取り入れるのが適切でしょう.
今回は試しに,「減る効果がねずみの数の2乗に比例する」と仮定して,以下の微分方程式を立ててみます.
先程の(3)式の右辺に,新たな項が加わっただけの式2ですね.
この式は,u(t)の増減率(左辺)が,u(t)に比例する増加の効果(右辺第一項)と,u(t)の二乗に比例する減少の効果(右辺第二項)の和で決まる,という意味です.
(αは先程と同じく単なる定数(増殖率)で,今回新しく出てきたβは,混雑定数と呼ばれる,これまた単なる定数です.)
この式は,ロジスティック方程式と呼ばれます.
ロジスティック方程式は,運良く解くことができて,あるタイミングにおけるねずみの数は以下のようになることが分かっています.
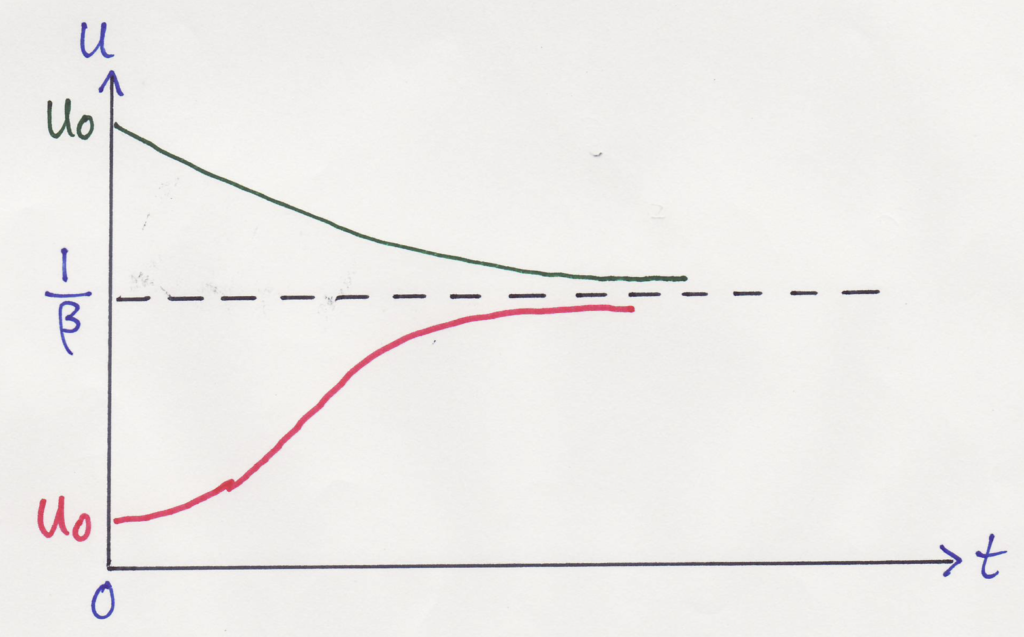
これを,分かりやすくグラフにしたものが下の図で,2つの場合についてそれぞれ描かれています.
はじめのねずみの数u(0)が1/βよりも多い場合には単調にねずみが減少し(黒線),少ない場合はS字のカーブを描きます(赤線).
そして,どちらの場合も,徐々に1/βに近づいていく(漸近していく)ということが分かります.
ねずみが永遠に増殖することはなくなり,より現実的な結果が得られました.
今回もまた,微分方程式という素晴らしいツールのおかげで,将来を予測することができましたね.
しかし,実は,どんな微分方程式もこううまくいくわけではありません.
(5)式のような「ある瞬間瞬間での数の増減のルール」が分かったからといって,直ちに(6)式のような一般解,すなわち,任意のタイミングでの数を予測できる式が得られるわけではないのです.
微分方程式の中には,一般解が得られれば,あるいはその存在の有無が分かるだけで,100万ドルの懸賞金をもらえるものもあります.
それ程に微分方程式は奥が深いのです.
カオス,フラクタル,ソリトン —より深い非線形の世界へ—
今回はこの辺で終わらなければなりませんが,講義ではここからさらに,より深い非線形の数理の世界へと話が展開されていきます.
カオスの話と天気予報の限界について.
マンデルブロ(下の図参照)のようなフラクタル図形について.
粒子性を持った波,ソリトンについて.
どれもとても興味深く,引き込まれる世界です.
理系大学1,2年生向けの講義ですので、高校-大学初頭にかけての数学知識がないと理解できないところも一部あるかもしれません.
しかし,先生が必ず最後に大事なことをまとめられているので、そこだけ聞いても十分楽しめるかと思います.
ぜひ,数理の世界を,覗いてみてください.
1ここでの増加率とは,単位時間あたりの増加数のことを意味します.全体に対する増加数の割合という意味ではありません.
2講義では少し異なった形で紹介されていますが,(3)式との対応を見やすくするため,あえてこの形にしています.
今回紹介した講義:数理の世界-新世紀の数学を探る(学術俯瞰講義)第2回 現象の数理
今回紹介した講義:数理の世界-新世紀の数学を探る(学術俯瞰講義)第3回 非線形の世界
●他の講義紹介記事はこちらから読むことができます。
<文/佐藤 瞭(東京大学オンライン教育支援サポーター)>