学術俯瞰講義「社会の形成― 人間はいかに共生してきたか」から、第10回『政府のいない社会における共生?』です。講師は、情報学環・学術情報学府の田中明彦(たなかあきひこ)先生です。
もし政府が存在しなかったら
私たちにとって政府とは
みなさんは“政府”をどのようなものとして捉えていますか?政府の役割はさまざまであり、一言で表すことは難しいですが、“政府”はいわば“リーダー”であり、私たちに指示をする存在であるということができます。
具体的には、“法律”などのルールを作り、人々を上からコントロールするということです。場合によってはそのルールに違反したものに罰則を与えるような役割を果たすこともあります。つまり、政府は人々の集団に秩序を与える存在であると定義することができます。
政府が存在しないとどうなる?
このようなリーダーとしての立ち回りを担う政府が存在しない世界を想像したことがあるでしょうか。“政府が存在しない”という状況を考える上での個々の行動はどのように帰結するのでしょうか。全体としての秩序は生まれるのかなど、さまざまな疑問が浮かび上がります。
本講義では、“人々の集団は政府が存在しない社会においてどのような行動を示すのだろうか”というテーマを、さまざまなモデル、理論を基に考えていきます。我々にとって当たり前のものとして存在する“政府”を改めて見つめ直し、私たち人間にとっての“共生”について深く考えてみましょう。
具体例からみつめる共生
シェリングの分居モデルから考える
いきなりですが具体例から先にお見せします。以下の写真はコンピュータ上のあるプログラムを作動させてランダムな赤と青の丸を動かしているものです。
(図は左→右の順番で変化)
プログラムに任せて赤丸と青丸を動かし続けると、最初はランダムに並んでいた丸たちが、徐々に各々の色どうしでまとまるようになり、ある種の秩序が生まれていくように見えることがお分かりいただけると思います。
このモデルはシェリングの分居モデルといわれるものであり、タイプの違う人間たちがそれぞれ違ったところに棲み分けをする様子を示しています。例えば、日本人と中国人が混在する地域において、どのように日本人街と中国人街が出現するかなどを、このモデルを用いて検証することができます。では、このモデルはそもそもどのような原理で動いているのでしょうか。
分居モデルの原理
このモデルにおいては、人と人を分けるある種の“差別”の原理が働いています。ただ、ここでいう差別は悪人のようなロジックに依拠したものではありません。このモデルにおける個人(写真でいう赤丸や青丸)は、自分の周りにどういった人間がいるかを確認し、行動をします。具体的なルールは以下の通りです。
・自分の周囲をみて、どういう人がいるか確認する
・ある程度以上、自分と同類がいればそこに留まる
・ある程度以上、自分と同類の人がいなければ、別のところにうつる
これらのルールにおける“ある程度以上”という水準は、それぞれの人間がその場に留まるか・移動するかの許容水準であり、これは仲間レートと呼ばれます。これらの要素を改めて整理すると、シェリングのモデルは以下のように説明することができます。
<シェリングのモデル>
・2種類の人間がいる
・それぞれがとどまる許容水準(仲間レート)がある
・仲間レートを超えると移動する
・仲間レートが高いと、分居が進むと予想される
・仲間レートが低いと、分居はすすまない
それでは、個々人の差別意識、つまり仲間レートが低ければ差別的環境は生まれないのでしょうか。講義動画内では、プログラムにさまざまな数字を当てはめて検証がなされており、ある意外な結果を得ることとなります。仲間レートをどれほどまでに下げれば分居が進まず、多様な人々が散らばって共生するような状況になるのでしょうか。詳しくは講義動画をご覧ください。
分居モデルの具体例
それではここで、シェリングの分居モデルを用いて具体的な話を一つ紹介したいと思います。例えば、喫煙者と禁煙者をきちんと分けて分煙を進めるためにはどうしたら良いでしょうか。この場合における目的は分煙、つまり”分かれる”ことであるため、喫煙者・禁煙者、お互いの差別意識が高く、仲間レートが高ければ分煙が進むという考えです。
ただ、コンピュータのプログラムを使って、仲間レートを高く設定したときの個々人の動きを検証すると、意外な結果が得られます。仲間レートを高く設定しているのにもかかわらず、なかなか分居が進まないのです。それどころか、いつまで経っても個々人が移動を続けてまったく定まりません。ただ、この結果をよく考えてみると、個々人が定位置につかない理由が納得できると思います。仲間レートを非常に高く設定しているために、周りに一人でも自分と違う人間がいる場合、その個人は移動することになってしまうのです。
つまり、例えば禁煙者Aの周りのほとんどが同じ禁煙者であっても、一人でも喫煙者がいれば禁煙者Aは不満を抱きその場から移動するといった流れがあちこちで発生するため、各人の場所が全く定まらずいつまでも動き続けることになるのです。このような、多数のエージェント(上記の例の場合、禁煙者・喫煙者)がそれぞれのルールを基に、相互作用するとき何が生じるのかを確かめる手法をマルチエージェントシュミレーションと呼び、さまざまな事例を検証するうえで用いられています。
合理的な行動とは?
これまでマクロな視点で多様な状況における個々人の行動を観察してきましたが、今からは、より基礎的なこととして、”そもそも個人が行動を合理的に決めるとはどういうことか”について、よりミクロな視点で観察していきます。
それに加えて、“複数が合理的な行動をすると何が起こるか・それは無政府社会においてどのような帰結をもたらすか”についても考察していきます。
合理的意思決定のモデル
ミニマックスの基準
ー不確実性における意思決定ー
それでは、何が起こるか予測することのできない不確実な場合における合理的な意思決定の方法を傘を例に紹介します。
上の図から、傘を持っていくか否かの2つの選択肢と、雨か晴れかという要素により最終的に4通りの結果を得ることができます。それぞれの状況の良し悪しを具体的に点数で示したものが右の数字であり、ここでは数字が高いほどいい結果ということになります。
傘を持っていった、持っていかなかったそれぞれの場合における最悪の結果は(2)の傘を持っていって晴れだったときと、(1)の傘を持っていかなくて雨だったときです。ここで、両方の場合におけるそれぞれの最悪の結果比べ、良い方を選ぶと、(2)の傘を持っていって晴れだったときになります。
これら一連の流れは合理的意思決定の一つであり、最悪の状態を比べて、そのなかのマックスを選択するという手法であり、ミニマックスの基準と呼ばれています。傘の例の場合、ミニマックスの基準に当てはめると、“傘を持っていく”という選択が最も合理的であるといえます。
ただ、これは不確実な場合における状況であり、今の例に“降水確率”のような確実性のある要素が加わるとどうなるでしょうか。
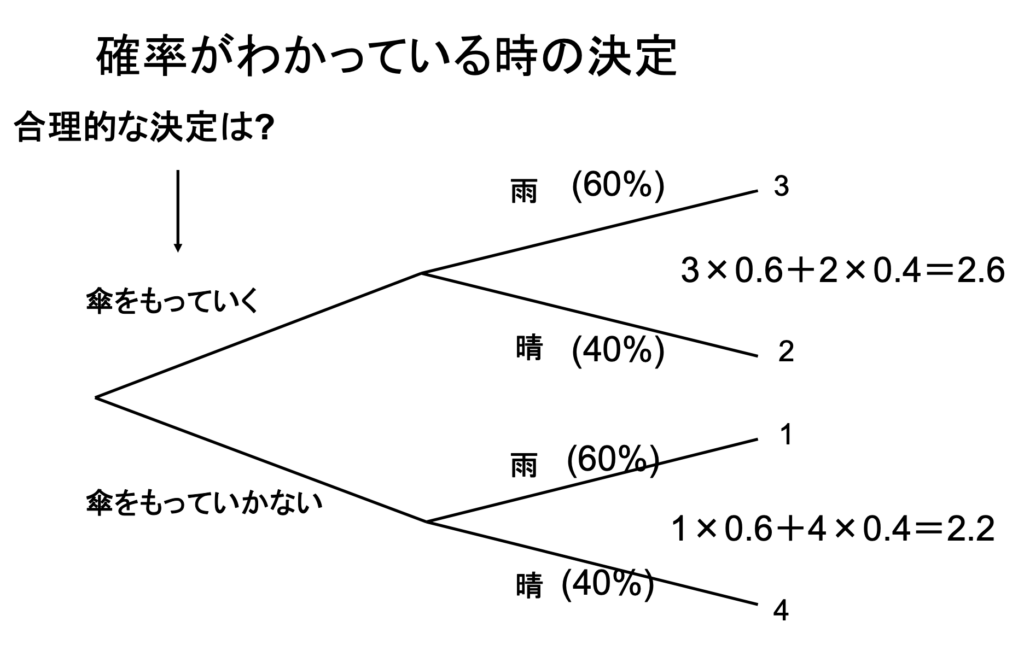
期待値最大化による合理的決定
ー確実性における意思決定ー
降水確率などの確実な要素がある場合、合理的決定がより具体的なものとなります。数学的な話はここでは省略しますが、図のように、より具体的な数字を算出し、それらを比べて合理的な意思決定を行います。この場合でも、”傘を持っていく”ことが合理的選択であるとわかります。
このように確実性がある場合における合理的意思決定を、期待値最大化による合理的決定といいます。
講義動画内においては、ミニマックスの基準、期待値最大化による合理的決定を真珠湾攻撃などの歴史的事実に当てはめてより具体的な検証が行われています。気になる方はぜひ動画をご覧ください。
合理的決定方法のジレンマ
いままで紹介した合理的意思決定方法は非常にロジカルで有効な場合もありますが、実際、問題点も存在します。まずは、そもそも決定論的世界はあまりないという点です。我々にできるのはあくまで予測であり、その予測は我々自身が決定した前提に基づくものです。事象が複合的に絡み合うプロセスを経たものが結果であるために、決定論的な世界は前提としてあまり存在しないのです。
そのため、確率を正確に付与できる場合も少なく、それに加えて、これまで二つの選択肢の中からどちらを選ぶかというやり方で合理的決定をしてきましたが、そもそも本当に選択肢が二つに帰着するのかという疑問も残ります。
つまり、合理的決定と言えど、どのような基準に依拠しているか、どのような選択肢を提示するかにより、結果が全く変わってくるのです。そのため、合理的決定それ自体に常に不確実性がつきまとうということがいえるのです。
相互作用と意思決定
多くの場合、人間は相互に相手の状態を考えながら決定を行うため、上記のような単純な手法では不十分です。そこで、ここからは複数の主体が合理的に相互作用した場合何がおきるのかについて考えていきます。
講義動画では、真珠湾攻撃やラバウル・ラエ輸送作戦など、歴史的事実を具体例に挙げて、複数の主体の相互作用を考慮したときの合理的意思決定方法について触れられています。
2種類のゲームの状況
ここからは、“ゲーム”における合理的意思決定についてご紹介します。まず、ここでいう
”ゲーム”の状況は以下の通りです。
ー相手がいる
ー相手の出方を考慮して自らの行動を決める(自分一人で勝手にやっているわけではない)
ー自分と相手の行動が相まって一つの結果が生じる
そして、相互作用がはたらくことを考慮したゲームの状況において行われる意思決定は
・ゼロサム・ゲーム的状況
・ノン・ゼロサム・ゲーム的状況
というように大きく2種類の場合に分けることができます。これらのゲームは、相手と自分の損得をどちらとも考慮した上で状況を区別する手法です。
しかしながら、これらの場合分けを行ったとしても常に十分な合理的意思決定を行うことはできないのです。その理由は、“相互作用”にあります。多くの状況において相互作用を要因とするジレンマが発生するために、確実な選択を行うことができないのです。
現代社会における合理的意思決定
ー均衡と調整ー
最後に“調整のゲーム”について紹介します。
このゲームは、自分だけが得するように選択を変えようとしても、得することができない状況であるという特徴があります。相手と自分の利益を相互に鑑みて合理的な意思決定を行うため、その意味での“調整”が行われるのです。調整が行われた結果、両者にとって最適な選択がとれる状況が“均衡”のとれた状況に落ち着くことができます。
この調整が行われる際、重要な鍵となる要素があります。それはずばり、”コミュニケーション”です。両者の意思疎通が図られることにより、互いの損得を認識し、スムーズに“調整”を行うことができるのです。このコミュニケーションを通じて、調整がなされるのと同時に秩序の発生もみられます。
調整のゲームと政府
調整のゲームはさまざまな場面において適用させることができるために、合理的意思決定において非常に有効な手段だということができます。
このゲームはコミュニケーションができれば実行することができるというメリットも持ち合わせています。それに加えて、コミュニケーションを通じて秩序が生まれるという特性もあります。これらを鑑みるに、記事冒頭で述べた法律の制定などにより秩序をつくるという政府の役割が、調整のゲームで秩序が発生するため、わざわざ政府が存在する意味がないのではないだろうかという疑問が生まれてきます。
ただ、調整のゲームにおいて政府はあると便利な存在であるということができます。理由としては、リーダーの役割を果たすものがいると、つまり指示を出す存在がいることとなるために秩序づくりをしやすくなるからです。この調整のゲームによる意思決定の合理性の精度をより高めるものとして、パレートの原理という原理があります。気になる方は講義動画をのぞいて、その原理がどのようなものかを学んでみてください。
まとめ
合理的な意思決定を行うための手法が数多く存在することをご理解いただけたでしょうか?
共生、相互作用など、さまざまな観点から合理的意思決定について触れてきましたが、実際にはどのような手法においても事象を取り巻く要素の不確実性が付随するために、確実に合理的な決定を選択するというのは難しい場合が多いのです。
当記事においては紹介することのできなかった具体例などが講義動画内においては多く紹介されています。ご興味のある方は是非動画をご覧になって、意思決定の“合理性”の奥深さ、そして私たちの“共生”をカタチ作る要素についてを追求してみてはいかがでしょうか。
<文/悪七一朗(東京大学学生サポーター)>
今回紹介した講義:社会の形成-人間はいかに共生してきたか(学術俯瞰講義) 第10回 政府のない社会における共生? 田中明彦先生
●他の講義紹介記事はこちらから読むことができます。